SIFT算法图像特征提取

SIFT(Scale-invariant feature tranform)是一种检测局部特征的算法，该算法通过求一幅图中的特征点及其有关Scale和orientation的描述子得到特征并进行图像特征点匹配。SIFT特征具有尺度不变性，即使改变旋转角度，图像亮度或拍摄视角，仍然能够得到好的检测效果。

算法原理及实现

1. 构建尺度空间

构建尺度空间时初始化操作，其目的是模拟图像数据的多尺度特征。采用高斯卷积核实现尺度变换：

$L(x,y,\sigma) = G(x,y,\sigma) * I(x,y)$ $G(x,y,\sigma) = \frac{1}{2\pi\sigma^2} e^{-\frac{x^2+y^2}{2\sigma^2}}$

其中 $G(x,y,\sigma)$ 是尺度可变高斯函数。$\sigma$ 大小决定图像的平滑程度。为了有效地在尺度空间检测到稳定的关键点，提出了高斯查分尺度空间(DoG scale-space)。即：

建立图像金字塔

对于一幅图像I，建立其在不同尺度(scale)的图像(octave)。为避免在检测极值点钱对原始图像的高斯平滑导致图像丢失高频信息，建议在建立尺度空间前首先对原始图像长宽扩展一倍，以保留原始图像信息，增加特征点数量。

第一个octave为图像的4倍，每一层图像尺度为$ (\sigma, k\sigma, k^2\sigma, k^3\sigma, k^4\sigma …) $，在本次实验中不失一般性取五层。之后的每一个octave都是前一个octave的$\frac{1}{4}$（长宽各减半）。得到尺度变换空间后，对每一个octave的相邻的图像求DoG得到最后的图像金字塔。

2. 寻找特征点

这里有两种方法来寻找特征点。

2.1 Harris角点检测

在图像金字塔中，对每一张图片计算Harris角点。这里可以直接调用opencv内置函数：

cv2.goodFeaturesToTrack(image, maxCorners, qualityLevel, minDistance[, corners[, mask[, blockSize[, useHarrisDetector[, k]]]]])   -> corners
Image: 输入图像
maxCorners: 允许返回的最多角点个数
qualityLevel: 角点质量，一般取0.01或0.001
minDistance = 10
blockSize = 3
k = 0.04

2.2 Hessian关键点检测

2.2.1 尺度空间极值点提取

对于D(x,y,d)中的某一个点，如果他在以他为中心的3x3x3立方体是最大值或最小值，则该点是一个极值点。

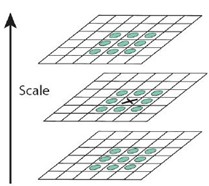
对这个点选取同一个octave相邻尺度DoG空间中的相邻的26个点进行比较。

2.2.2 对比度检测

若对比度的绝对值小于0.03就将这个点丢弃。

def calcTrst(src, x, y):
	local = src[x-1: x+2, y-1: y+2]
	std = local.std()
	mean = local.mean()
	if std == 0:
		return False
	else:
		return abs((src[x][y] - mean) / std) > 0.3

2.2.3 去除边缘响应

由计算可得， 为了检测主曲率是否在某阈值r下，只需检测

实际中一般取r=10。可以使用scipy来对图像进行求导操作，示例如下：

import numpy as np
from scipy.ndimage import filters

sigma = 5

imx = zeros(im.shape)
filter.gaussian_filter(im, (sigma, sigma), (0, 1), imx)
imy = zeros(im.shape)
filter.gaussian_filter(im, (sigma, sigma), (1, 0), imy)

Note: 由于时间原因我采用第一种方法完成SIFT算法，第二种方法写了一点但是还没有写完，在hessian.py中。

3. 寻找特征点的主方向

利用关键点领域像素的梯度方向分布特性为每个关键点指定方向参数，使算子具备旋转不变性。

$m(x,y)=\sqrt{(L(x+1,y)-L(x-1,y))^2+(L(x,y+1)-L(x,y-1))^2}$ $\theta (x,y)= a \tan{2\frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)}}$

实际计算时，我们在以关键点为中心的领域窗口内采样，并用直方图统计领域像素的梯度方向。梯度直方图的范围是0-360度，其中每10度一个柱，每一个在该范围区间内的点都具有模值的权重。直方图的峰值泽作为该关键点处领域的主方向，即作为该关键点的方向。

def getMainDirect(grads, corners):
    sigma = 1
    pillar_directs = transDirects(grads, 36)
    directs = []
    gs = GSmodel(sigma)
    r = (gs.shape[0] - 1) / 2
    for i in range(len(grads)):
        directs.append([])
        for x0, y0 in corners[i]:
            wei_grad = grads[i][0, y0 - r: y0 + r + 1, x0 - r: x0 + r + 1] * gs
            direct = np.bincount(pillar_directs[i][y0-r: y0+r+1, x0-r: x0+r+1].ravel(), wei_grad.ravel(), minlength=36)
            grad_limit = direct.max() * 0.8
            for j in range(36):
                if direct[j] >= grad_limit:
                    directs[i].append((x0, y0, math.pi * (j - 18) / 18.0))
    return directs

4. 生成关键点描述子

将坐标轴旋转为关键点的方向，以确保旋转不变性。以关键点为中心取8x8的窗口。

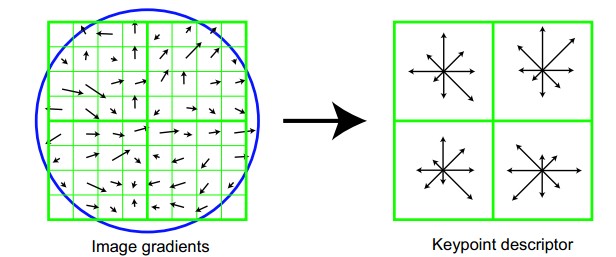
在每4×4的小块上计算8个方向的梯度方向直方图，绘制每个梯度方向的累加值，即可形成一个种子点，如图右部分示。此图中一个关键点由2×2共4个种子点组成，每个种子点有8个方向向量信息。这样就可以对每个feature形成一个448=128维的描述子，每一维都可以表示4*4个格子中一个的scale/orientation.，最后将这个向量归一化。

5. 根据SIFT进行Match

当两幅图像的SIFT特征向量生成后，下一步我们采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取图像1中的某个关键点，并找出其与图像2中欧式距离最近的前两个关键点，在这两个关键点中，如果最近的距离除以次近的距离少于某个比例阈值，则接受这一对匹配点。降低这个比例阈值，SIFT匹配点数目会减少，但更加稳定。

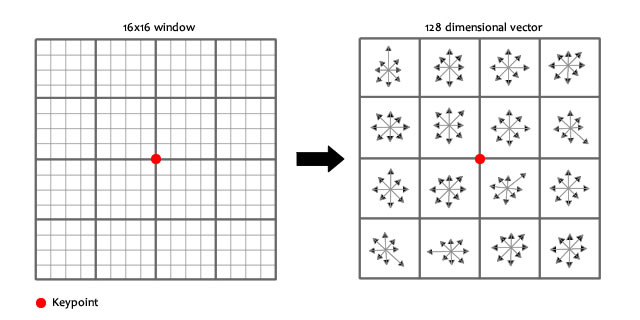
实际计算过程中，为了增强匹配的稳健性，Lowe建议对每个关键点使用4×4共16个种子点来描述，这样对于一个关键点就可以产生128个数据，即最终形成128维的SIFT特征向量。此时SIFT特征向量已经去除了尺度变化、旋转等几何变形因素的影响，再继续将特征向量的长度归一化，则可以进一步去除光照变化的影响。 当两幅图像的SIFT特征向量生成后，下一步我们采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取图像1中的某个关键点，并找出其与图像2中欧式距离最近的前两个关键点，在这两个关键点中，如果最近的距离除以次近的距离少于某个比例阈值，则接受这一对匹配点。降低这个比例阈值，SIFT匹配点数目会减少，但更加稳定。为了排除因为图像遮挡和背景混乱而产生的无匹配关系的关键点,Lowe提出了比较最近邻距离与次近邻距离的方法,距离比率ratio小于某个阈值的认为是正确匹配。因为对于错误匹配,由于特征空间的高维性,相似的距离可能有大量其他的错误匹配,从而它的ratio值比较高。Lowe推荐ratio的阈值为0.8。但作者对大量任意存在尺度、旋转和亮度变化的两幅图片进行匹配，结果表明ratio取值在0. 4~0. 6之间最佳，小于0. 4的很少有匹配点，大于0. 6的则存在大量错误匹配点。(如果这个地方你要改进，最好给出一个匹配率和ration之间的关系图，这样才有说服力)作者建议ratio的取值原则如下:
ratio=0. 4　对于准确度要求高的匹配；
ratio=0. 6　对于匹配点数目要求比较多的匹配；
ratio=0. 5　一般情况下。
也可按如下原则:当最近邻距离<200时ratio=0. 6，反之ratio=0. 4。ratio的取值策略能排分错误匹配点。